
Total-Variation — Fast Gradient Flow and Relations to Koopman Theory
Ido Cohen et al. The space-discrete Total Variation (TV) flow is analyzed using several mode decomposition techniques. In the one-dimensional case, we provide analytic formulations to Dynamic Mode Decomposition (DMD) and to Koopman Mode Decomposition (KMD) of the TV-flow and compare the obtained modes to TV spectral decomposition. We propose a computationally efficient algorithm to […]
Examining the Limitations of Dynamic Mode Decomposition through Koopman Theory Analysis
Ido Cohen and Guy Gilboa This work binds the existence of Koopman Eigenfunction (KEF), the geometric of the dynamics, and the validity of DMD to one coherent theory. Viewing the dynamic as a curve in the state-space allows us to formulate an existence condition of KEFs and their multiplicities. These conditions lay the foundations for […]
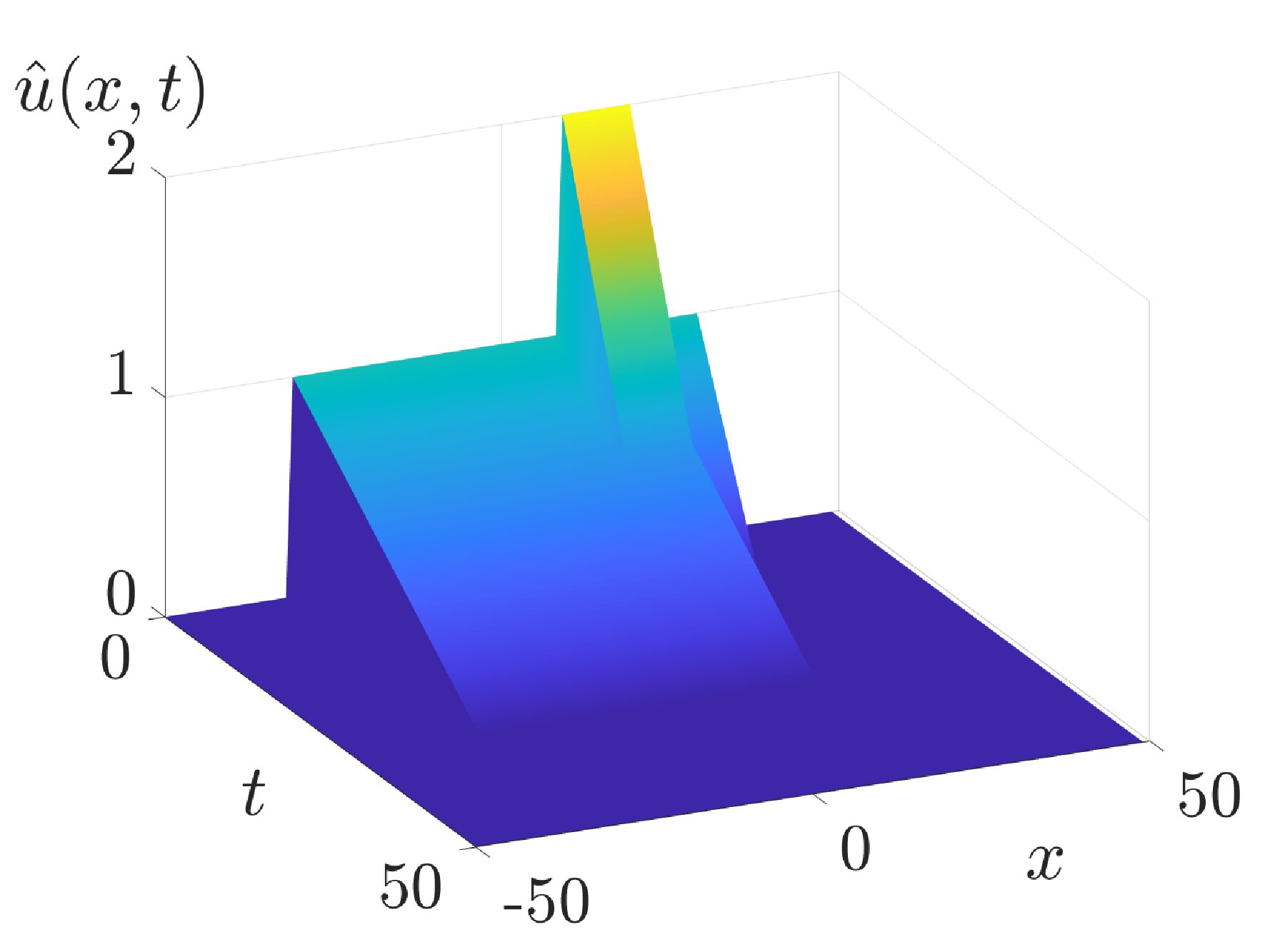
Total-Variation Mode Decomposition
Ido Cohen et al. SSVM In this work, we analyze the Total Variation(TV) flow applied to one-dimensional signals. We formulate a relation between Dynamic Mode Decomposition(DMD), a dimensionality reduction method based on the Koopman operator and the spectral TV decomposition. DMD is adapted by time rescaling to fit linearly decaying processes, such as the TV […]
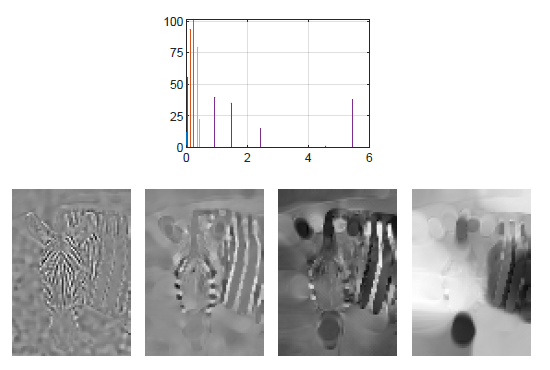
Modes of Homogeneous Gradient Flows
Ido Cohen et al. SIAM Finding latent structures in data is drawing increasing attention in diverse fields such as image and signal processing, fluid dynamics, and machine learning. In this work we examine the problem of finding the main modes of gradient flows. Gradient descent is a fundamental process in optimization where its stochastic version […]

Introducing the p-Laplacian Spectra
Ido Cohen and Guy Gilboa Signal Processing In this work we develop a nonlinear decomposition, associated with nonlinear eigenfunctions of the p-Laplacian for p ∈ (1, 2). With this decomposition we can process signals of different degrees of smoothness. We first analyze solutions of scale spaces, generated by γ-homogeneous operators, γ∈R. An analytic solution is formulated when the scale space […]
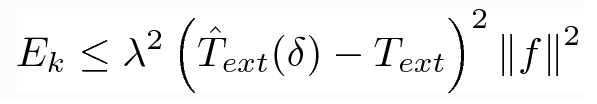
Stable Explicit p-Laplacian Flows Based on Nonlinear Eigenvalue Analysis
Ido Cohen, Adi Falik and Guy Gilboa SSVM 2019 Implementation of nonlinear flows by explicit schemes can be very convenient, due to their simplicity and low-computational cost per time step. A well known drawback is the small time step bound, referred to as the CFL condition, which ensures a stable flow. For p-Laplacian flows, with 1<p<21<p<2, explicit […]
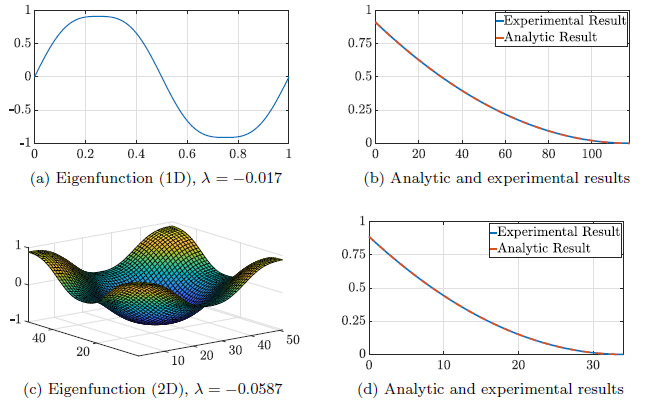
Shape Preserving Flows and the p−Laplacian Spectra
Ido Cohen and Guy Gilboa HAL We examine nonlinear scale-spaces in the general form ut = P (u(t)), where P is a bounded nonlinear operator. We seek solutions with separation of variables in space and time u(x, t) = a(t)f (x), where f is the initial condition. We term these as shape-preserving flows and provide […]
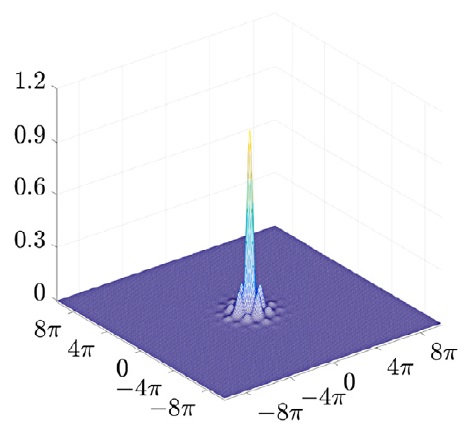
Energy Dissipating Flows for Solving Nonlinear Eigenpair Problems
Ido Cohen and Guy Gilboa Journal of Computational Physics This work is concerned with computing nonlinear eigenpairs, which model solitary waves and various other physical phenomena. We aim at solving nonlinear eigenvalue problems of the general form T(u)=λQ(u). In our setting T is a variational derivative of a convex functional (such as the Laplacian operator with respect to […]
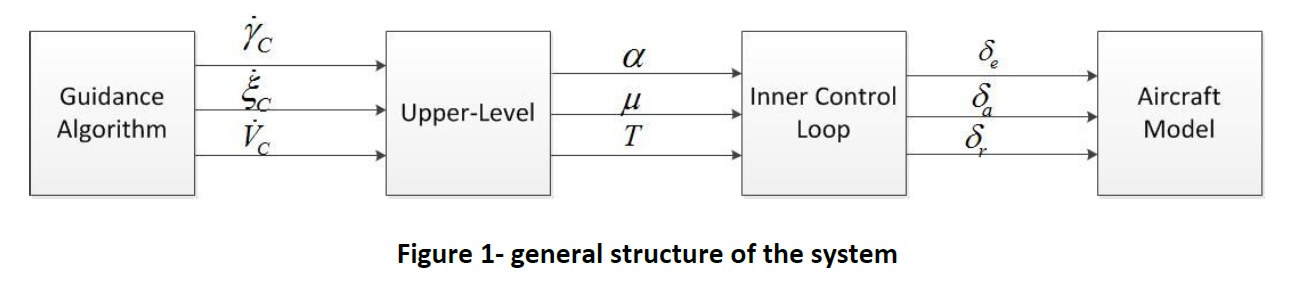
Control and Guidance of Fighter Aircraft in Autonomic Flight
M.Sc. dissertation In this thesis we propose a control and guidance system for the autonomous execution of agile flight maneuvers, similar to those performed by a combat pilot and which utilize the entire lift capabilities of the aircraft while taking into account their limitations. This work has been motivated by applications to combat flight simulators, […]

