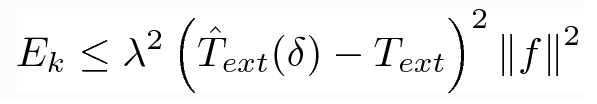Ido Cohen, Adi Falik and Guy Gilboa SSVM 2019

Implementation of nonlinear flows by explicit schemes can be very convenient, due to their simplicity and low-computational cost per time step. A well known drawback is the small time step bound, referred to as the CFL condition, which ensures a stable flow. For p-Laplacian flows, with 1<p<21<p<2, explicit schemes without gradient regularization require, in principle, a time step approaching zero. However, numerical implementations show explicit flows with small time-steps are well behaved. We can now explain and quantify this phenomenon.

In this paper we examine explicit p-Laplacian flows by analyzing the evolution of nonlinear eigenfunctions, with respect to the p-Laplacian operator. For these cases analytic solutions can be formulated, allowing for a comprehensive analysis. A generalized CFL condition is presented, relating the time step to the inverse of the nonlinear eigenvalue. Moreover, we show that the flow converges and formulate a bound on the error of the discrete scheme. Finally, we examine general initial conditions and propose a dynamic time-step bound, which is based on a nonlinear Rayleigh quotient.