
Total-Variation — Fast Gradient Flow and Relations to Koopman Theory
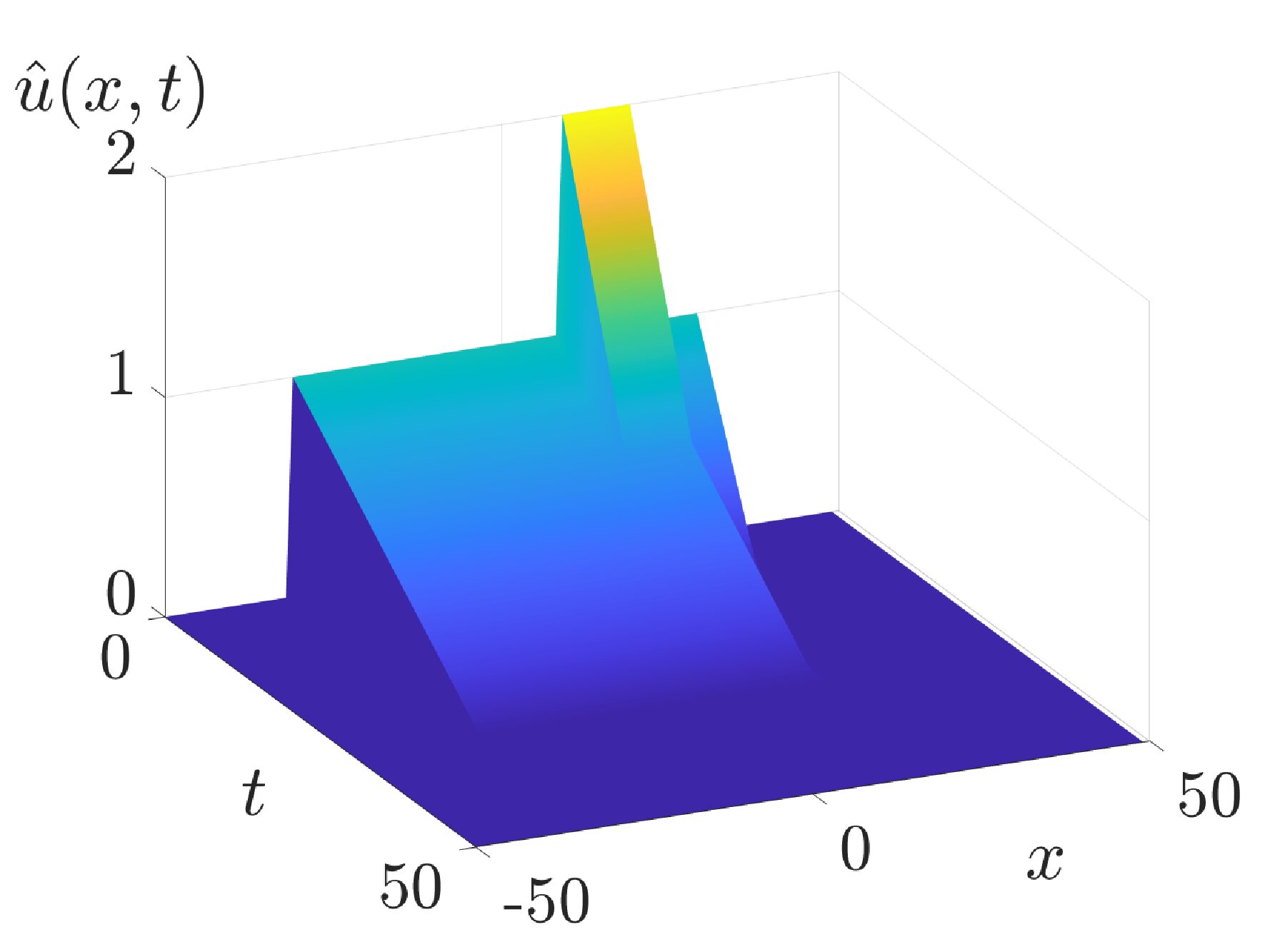
Ido Cohen et al. The space-discrete Total Variation (TV) flow is analyzed using several mode decomposition techniques. In the one-dimensional case, we provide analytic formulations to Dynamic Mode Decomposition (DMD) and to Koopman Mode Decomposition (KMD) of the TV-flow and compare the obtained modes to TV spectral decomposition. We propose a computationally efficient algorithm to […]
Examining the Limitations of Dynamic Mode Decomposition through Koopman Theory Analysis
Ido Cohen and Guy Gilboa This work binds the existence of Koopman Eigenfunction (KEF), the geometric of the dynamics, and the validity of DMD to one coherent theory. Viewing the dynamic as a curve in the state-space allows us to formulate an existence condition of KEFs and their multiplicities. These conditions lay the foundations for […]
Total-Variation Mode Decomposition
Ido Cohen et al. code In this work we analyze theTotal Variation(TV) flow ap-plied to one dimensional signals. We formulate a relation between Dynamic Mode Decomposition(DMD), a dimensionality reduction method basedon the Koopman operator, and the spectral TV decomposition. DMD isadapted by time rescaling to fit linearly decaying processes, such as theTV flow. For the […]

